IBM Quantum Challenge 2020 - Part 6
This post is part of a serie of posts on my experience with the IBM Quantum Challenge 2020.
The serie is organised as follow:
- Introduction to the problem.
- Mathematical reformulation of the problem.
- Unoptimised implementation of the solution.
- How to optimise a quantum circuit?.
- Optimising multi-controlled
Xgates. - Optimising the
QRAM(this post).
In this blog post I detail the two optimisations I used to lower
down significantly the cost of the QRAM implementation.
40k - Re-using computations by using an ancilla qubit
In the non-optimised version, we implemented the QRAM by chaining the following quantum circuit for all the possible indices (from 0 to 15 included) by changing the $X$ gates sandwiching the 4-controlled $X$ gates:
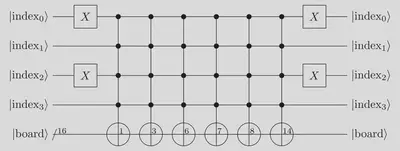
But this quantum circuit is far from optimal. Instead of applying independently the six 4-controlled $X$ gates we could save in one ancilla qubit the result of one of the 4-controlled $X$ operation and then broadcast this result using six 1-controlled $X$ gates.
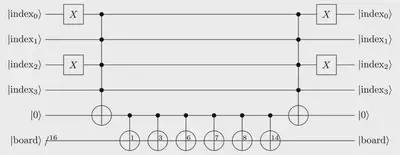
This is done by changing the implementation of the qram and
encode_problem functions:
def encode_problem(problem: BoardEncoding) -> QuantumCircuit:
"""
Encode the given problem on the qboard register if the
qstate register is in the |1> state.
This function returns a quantum circuit that encodes the given problem
on the |qboard> register only if the |qstate> register is |1>.
:param problem: a list of asteroid coordinates, given as tuples
of strings.
"""
qboard = QuantumRegister(16)
qstate = QuantumRegister(1)
circuit = QuantumCircuit(qboard, qstate, name="encode_problem")
for x, y in problem:
index = 4 * int(x) + int(y)
circuit.cx(qstate[0], qboard[index])
return circuit
def qram(problem_set: ty.List[BoardEncoding]):
"""
Encodes the given problem set into the |qboard> register.
The returned routine takes as inputs:
- |qindex> that encodes the indices for which we want to encode the
boards. The |qindex> register will likely be given in a
superposition of all the possible states.
- |qboard> that should be given in the |0> state and that is returned
in the state that encodes the problem_set given. For each qindex,
the |qboard> state in |qindex>|qboard> is full of |0> except on the
locations where there is an asteroid, in which case the state is |1>.
- |qancilla> that is a 3-qubit ancillary register.
"""
qindex = QuantumRegister(4)
qboard = QuantumRegister(16)
qstate = QuantumRegister(1)
qancilla = QuantumRegister(2)
circuit = QuantumCircuit(qindex, qboard, qstate, qancilla, name="qram")
for i, problem in enumerate(problem_set):
bin_str = bin(i)[2:].zfill(4)
x_qubits = [j for j in range(4) if bin_str[j] == "0"]
# setting qstate to |1> if we are in the index "i".
if x_qubits:
circuit.x([qindex[j] for j in x_qubits])
circuit.mcx(qindex, qstate, ancilla_qubits=qancilla, mode="v-chain")
circuit.append(encode_problem(problem), [*qboard, *qstate])
# Undo the qstate thing
circuit.mcx(qindex, qstate, ancilla_qubits=qancilla, mode="v-chain").inverse()
if x_qubits:
circuit.x([qindex[j] for j in x_qubits]).inverse()
return circuit
The functions using these methods should also be modified to account for the extra qubit added as an ancilla. The final code implementing this optimisation is available on this Gist.
28k - Advanced looping through all the integer values on 16 qubits
The optimisation presented in the last section allowed me to
nearly halve the number of calls to the mcx_vchain procedure due
to the QRAM, which is great! But as seen in the call-graph below,
the QRAM still performs nearly 34% of the mcx_vchain calls,
which is too high.
At this point in the optimisation process I had only one optimisation idea left for the QRAM: using Gray codes or something similar. The main idea is the following: as we know for sure we need to loop over all the $16$ possible integers in the QRAM, maybe I could rearrange the way I loop through them in order to avoid some multiply-controlled gates?
Re-phrasing our QRAM problem, we basically want to implement an
operation known as Select(V) that implements
$$ \mathrm{Select}(V) = \sum_{i=0}^{15} \vert i \rangle \langle i\vert \otimes V_i $$
where $V_i$ is a quantum circuit encoding the $i$-th board. We
already have an efficient implementation for $V_i$ with the
encode_problem routine used in the previous section, the only
challenge left is to implement the Select(.) part.
Luckily for me, I was already aware of a very nice paper that was
discussing the implementation of the Select(.) part: Toward the
first quantum simulation with quantum speedup.
The algorithm is perfectly described in Section G.4. of the paper and implemented in https://github.com/njross/simcount. Sadly, because I was quite in a rush, my implementation is not generic at all and is rather specialised to the asteroid problem I was trying to solve. As such, the code is long and not necessarily easy to read.
def qram(problem_set: ty.List[BoardEncoding]):
"""
Encodes the given problem set into the |qboard> register.
The returned routine takes as inputs:
- |qindex> (called |x> in the implementation) that encodes the indices for
which we want to encode the boards. The |index> register will likely be
given in a superposition of all the possible states.
- |qboard> that should be given in the |0> state and that is returned in
the state that encodes the problem_set given.
For each qindex, the |qboard> state in |qindex>|qboard> is full of |0>
except on the locations where there is an asteroid, in which case the
state is |1>.
- |qancilla> (called |q> in the implementation) is a 3-qubit ancilla
register.
This implementation is using the "Select V" algorithm from
https://arxiv.org/abs/1711.10980. See Section G.4. and Figure 6.
Note: everything has been unrolled because I did not have the time to write
and debug the generic version of the algorithm. Sorry for this.
"""
x = QuantumRegister(4) # Index
qboard = QuantumRegister(16)
q = QuantumRegister(3)
circuit = QuantumCircuit(x, qboard, q, name="QRAM")
# Trick to have the same indices as in the paper
x = [None, *x[::-1]]
q = [1, x[1], *q]
# First, x[0] positive
circuit.rccx(q[1], x[2], q[2])
circuit.rccx(q[2], x[3], q[3])
circuit.rccx(q[3], x[4], q[4])
# q[4] is |1> only if the index was |1111>
circuit.append(encode_problem(problem_set[0b1111]), [*qboard, q[4]])
# Short-circuit (red)
circuit.cx(q[3], q[4])
# q[4] is |1> only if the index was |1110>
circuit.append(encode_problem(problem_set[0b1110]), [*qboard, q[4]])
# Short-circuit (green)
circuit.cx(q[3], q[4])
circuit.rccx(q[2], x[4], q[4])
circuit.cx(q[2], q[3])
# q[4] is |1> only if the index was |1101>
circuit.append(encode_problem(problem_set[0b1101]), [*qboard, q[4]])
# Short-circuit (red)
circuit.cx(q[3], q[4])
# q[4] is |1> only if the index was |1100>
circuit.append(encode_problem(problem_set[0b1100]), [*qboard, q[4]])
# Go up
circuit.x(x[4])
circuit.rccx(q[3], x[4], q[4])
circuit.x(x[4]).inverse()
# Short-circuit (green)
circuit.cx(q[2], q[3])
circuit.rccx(q[1], x[3], q[3])
circuit.cx(q[1], q[2])
# Go down
circuit.rccx(q[3], x[4], q[4])
# q[4] is |1> only if the index was |1011>
circuit.append(encode_problem(problem_set[0b1011]), [*qboard, q[4]])
# Short-circuit (red)
circuit.cx(q[3], q[4])
# q[4] is |1> only if the index was |1010>
circuit.append(encode_problem(problem_set[0b1010]), [*qboard, q[4]])
# Short-circuit (green)
circuit.cx(q[3], q[4])
circuit.rccx(q[2], x[4], q[4])
circuit.cx(q[2], q[3])
# q[4] is |1> only if the index was |1001>
circuit.append(encode_problem(problem_set[0b1001]), [*qboard, q[4]])
# Short-circuit (red)
circuit.cx(q[3], q[4])
# q[4] is |1> only if the index was |1000>
circuit.append(encode_problem(problem_set[0b1000]), [*qboard, q[4]])
# Go up
circuit.x(x[4])
circuit.rccx(q[3], x[4], q[4])
circuit.x(x[4]).inverse()
# Go up
circuit.x(x[3])
circuit.rccx(q[2], x[3], q[3])
circuit.x(x[3]).inverse()
# Short-circuit (green)
# Small trick here: we are supposed to use q[0] but q[0] is "virtual"
# and always equal to "1", so we can simplify.
circuit.cx(q[1], q[2])
circuit.cx(x[2], q[2]) # circuit.rccx(q[0], x[2], q[2])
circuit.x(q[1]) # circuit.cx(q[0], q[1])
# Go down
circuit.rccx(q[2], x[3], q[3])
# Go down
circuit.rccx(q[3], x[4], q[4])
# q[4] is |1> only if the index was |0111>
circuit.append(encode_problem(problem_set[0b0111]), [*qboard, q[4]])
# Short-circuit (red)
circuit.cx(q[3], q[4])
# q[4] is |1> only if the index was |0110>
circuit.append(encode_problem(problem_set[0b0110]), [*qboard, q[4]])
# Short-circuit (green)
circuit.cx(q[3], q[4])
circuit.rccx(q[2], x[4], q[4])
circuit.cx(q[2], q[3])
# q[4] is |1> only if the index was |0101>
circuit.append(encode_problem(problem_set[0b0101]), [*qboard, q[4]])
# Short-circuit (red)
circuit.cx(q[3], q[4])
# q[4] is |1> only if the index was |0100>
circuit.append(encode_problem(problem_set[0b0100]), [*qboard, q[4]])
# Go up
circuit.x(x[4])
circuit.rccx(q[3], x[4], q[4])
circuit.x(x[4]).inverse()
# Short-circuit (green)
circuit.cx(q[2], q[3])
circuit.rccx(q[1], x[3], q[3])
circuit.cx(q[1], q[2])
# Go down
circuit.rccx(q[3], x[4], q[4])
# q[4] is |1> only if the index was |0011>
circuit.append(encode_problem(problem_set[0b0011]), [*qboard, q[4]])
# Short-circuit (red)
circuit.cx(q[3], q[4])
# q[4] is |1> only if the index was |0010>
circuit.append(encode_problem(problem_set[0b0010]), [*qboard, q[4]])
# Short-circuit (green)
circuit.cx(q[3], q[4])
circuit.rccx(q[2], x[4], q[4])
circuit.cx(q[2], q[3])
# q[4] is |1> only if the index was |0001>
circuit.append(encode_problem(problem_set[0b0001]), [*qboard, q[4]])
# Short-circuit (red)
circuit.cx(q[3], q[4])
# q[4] is |1> only if the index was |0001>
circuit.append(encode_problem(problem_set[0b0000]), [*qboard, q[4]])
# Go up
circuit.x(x[4])
circuit.rccx(q[3], x[4], q[4])
circuit.x(x[4]).inverse()
# Go up
circuit.x(x[3])
circuit.rccx(q[2], x[3], q[3])
circuit.x(x[3]).inverse()
# Go up
circuit.x(x[2])
circuit.rccx(q[1], x[2], q[2])
circuit.x(x[2]).inverse()
# To avoid changing x[1]:
circuit.x(x[1])
return circuit
The code including this optimisation is available on this Gist.
The new call-graph is the following:
Waow! The QRAM is now only taking ~13% of the total cost of the
circuit. Compared to the check_if_match_any_permutation subroutine
that takes more than 85% of the total cost, I can say that the
QRAM optimisation has succeeded! At this point, I decided to put
my efforts into optimising the oracle instead of the QRAM because
of the cost difference.
In the next blog post I will explain how I optimised the very last subroutine that contributes greatly to the overall cost: check_if_match_any_permutation.